【人気ダウンロード!】 ��分数を仮分数に直す方法 466477-帯分数を仮分数に直す方法

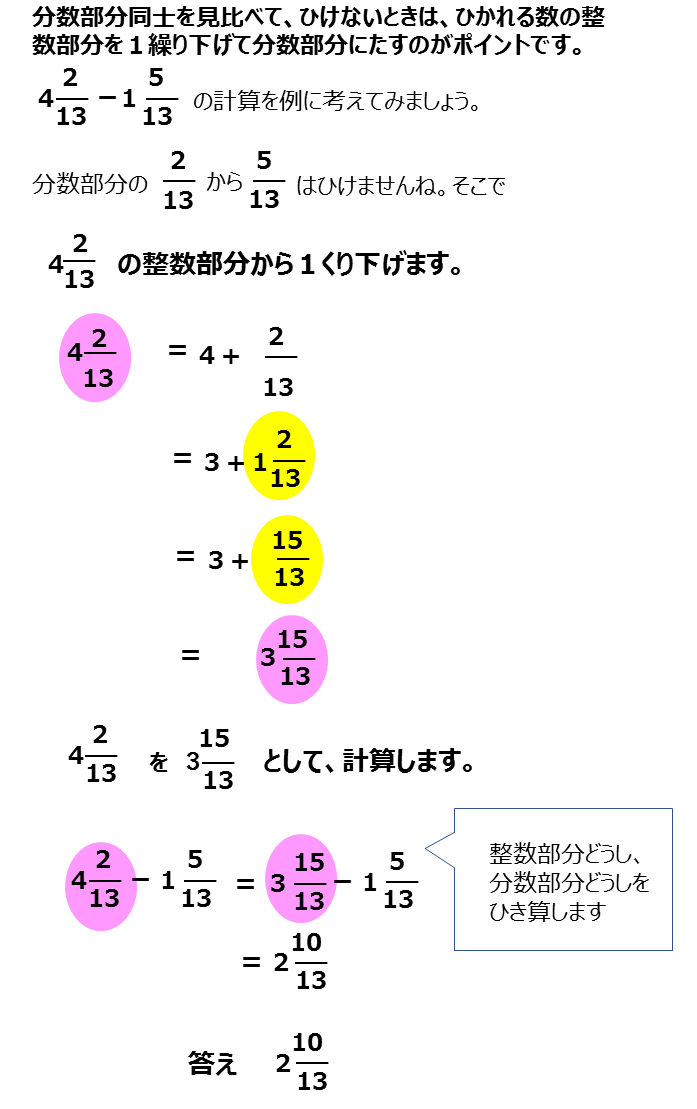
異なる分母の引き算 帯分数 5年生 分数の足し算 引き算 まなび365 無料算数プリント
その中でも、帯分数の絡むかけ算やわり算は、 帯分数を仮分数に直すこと そして、答が仮分数になれば、 仮分数を帯分数に直すこと があり、これが特にわずらわしいと思ったことでしょう。 しかし、中学生になれば、実は、このわずらわしさから、仮分数を帯分数に直す方法を教えます。 下の例をもとに説明します。 動画を使ってもう一度説明します 動画作成協力・・動くイラストフリー素材 下が答えになります 教え方2-③ 帯分数を仮分数に直す方法を教えます。 下の例を元に説明します。 動画
帯分数を仮分数に直す方法
帯分数を仮分数に直す方法-3 約分できる場合の分数のかけ算 31 かけ算をする前に約分をして数字を小さくする 仮分数を帯分数へ 算数嫌い解消! 算数ギライをなくす活動をしているゼロ先生です。 いつもお読み頂きありがとうございます。 もし、あなたが、4年生に仮分数を帯分数に直す方法を教えるとしたら、 どのようにしますか? 必ず指導しなければなら

分数のかけ算の計算プリント 帯分数編 全240問無料 算数パラダイス
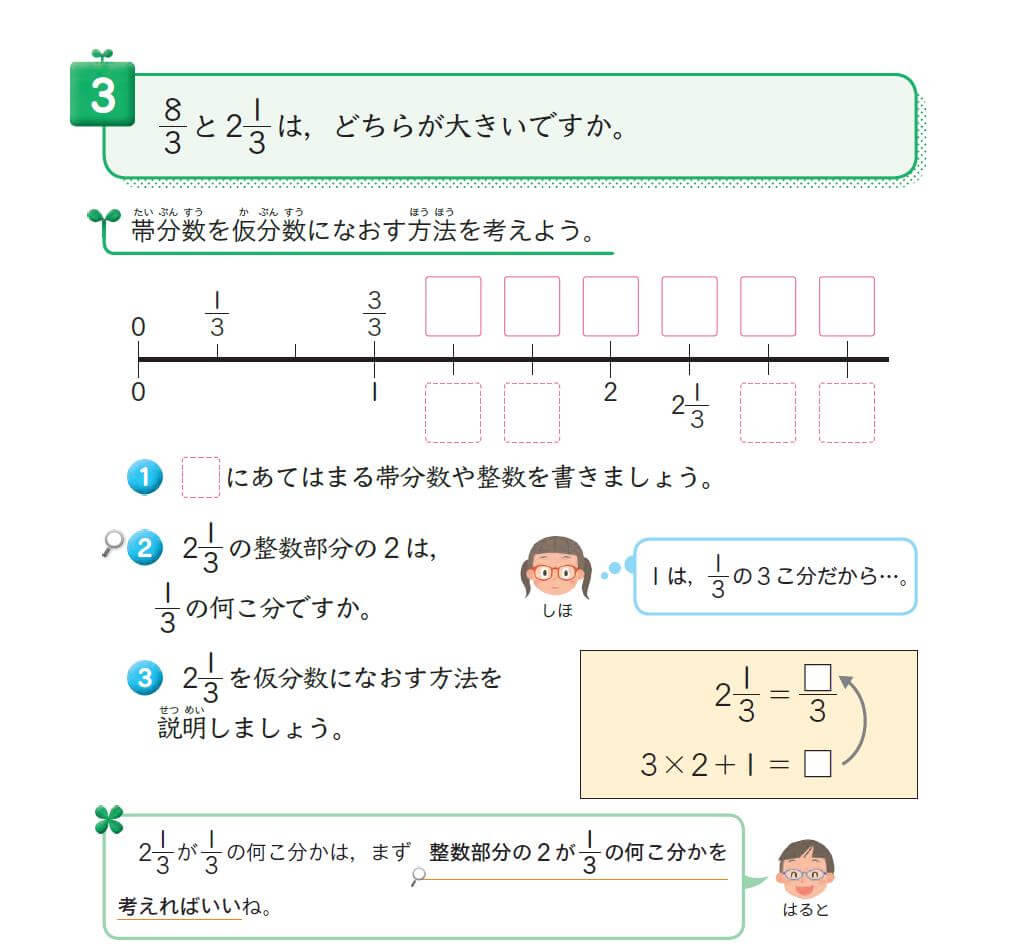
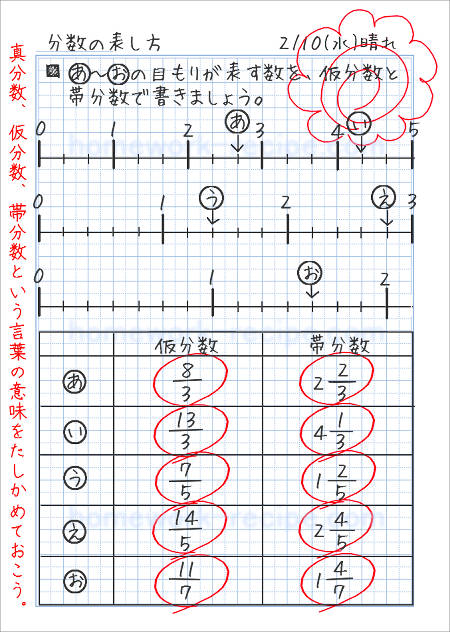
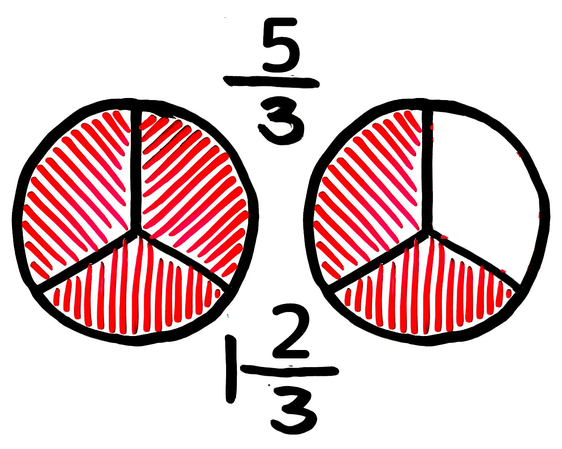
もくじ 1 分数と分数のかけ算の方法 11 整数と分数のかけ算では、整数を分数に直す; 仮分数を帯分数に直す方法 仮分数を帯分数に直す方法は、次のように行います。 仮分数を帯分数に直しましょう。 分子と分母を分けて計算します。分子÷分母=商・・・あまり; 帯分数から仮分数に直す方法は スライド11ページ から。 ピザを使った図を書いてみましょう。 帯分数は「整数と分数の組み合わせ」なので、 1と2/3なら、 ピザがまるまる1枚と、3等分されたピザ2枚分 ということになります。
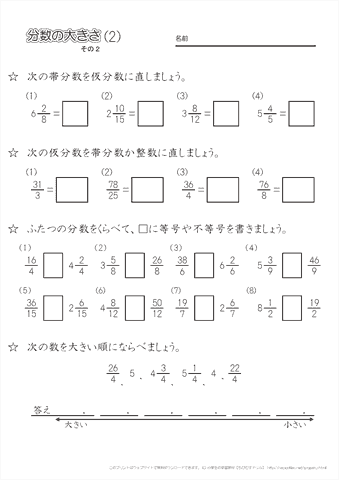
仮分数を帯分数になおすには,どうすればいいの 真分数と仮分数・帯分数と帯分数などの大きさをくらべる方法を教えて 10 仮分数と帯分数の大きさのくらべ方を教えて次の帯分数を仮分数になおしましょう。 6 3 = 39 7 1 8 8 6 6 9 9 7 6 0 (9) 52 = 5 (7) 19 = 2 3 (8) 36 = 3 3 9 9 7 7 4 4 3 (6) 46 = 6 (4) 26 = 8 2 (5) 39 = 2 2 5 5 4 4 0 6 3 (3) 8 = 2 次の仮分数を,帯分数か整数になおしましょう。 (1) 10 = 5 0 (2) 33 = 分数7 (仮分数・帯分数)整数と分数がくっついた帯分数。 帯分数を仮分数に直す方法 まずは、1を分数で表すとどうなるのか考えてみましょう。 つまり、分母の数と分子の数が同じならば「1」になります。では、他の整数はどうなるでしょうか。
帯分数を仮分数に直す方法のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 分数の計算方法を解説 分数は小数よりもずっとサボれる |  分数の計算方法を解説 分数は小数よりもずっとサボれる |  分数の計算方法を解説 分数は小数よりもずっとサボれる |
 分数の計算方法を解説 分数は小数よりもずっとサボれる | 分数の計算方法を解説 分数は小数よりもずっとサボれる | 分数の計算方法を解説 分数は小数よりもずっとサボれる |
 分数の計算方法を解説 分数は小数よりもずっとサボれる |  分数の計算方法を解説 分数は小数よりもずっとサボれる | 分数の計算方法を解説 分数は小数よりもずっとサボれる |
「帯分数を仮分数に直す方法」の画像ギャラリー、詳細は各画像をクリックしてください。
 分数の計算方法を解説 分数は小数よりもずっとサボれる |  分数の計算方法を解説 分数は小数よりもずっとサボれる |  分数の計算方法を解説 分数は小数よりもずっとサボれる |
分数の計算方法を解説 分数は小数よりもずっとサボれる | 分数の計算方法を解説 分数は小数よりもずっとサボれる |  分数の計算方法を解説 分数は小数よりもずっとサボれる |
分数の計算方法を解説 分数は小数よりもずっとサボれる |  分数の計算方法を解説 分数は小数よりもずっとサボれる | 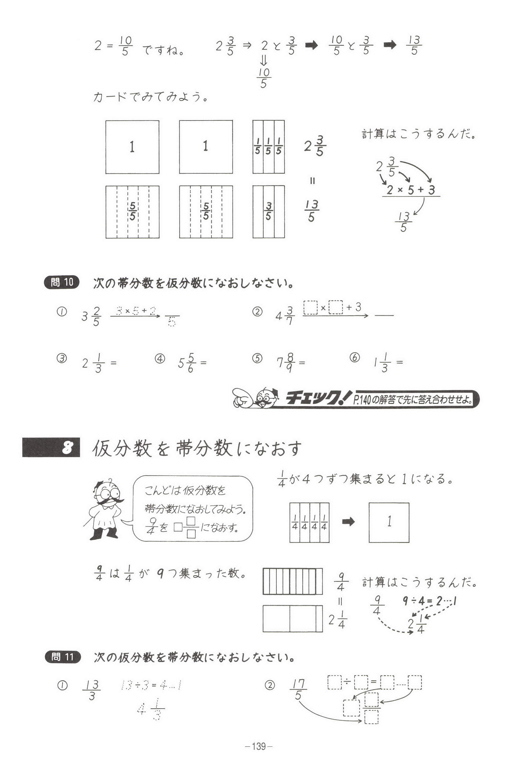 分数の計算方法を解説 分数は小数よりもずっとサボれる |
「帯分数を仮分数に直す方法」の画像ギャラリー、詳細は各画像をクリックしてください。
 分数の計算方法を解説 分数は小数よりもずっとサボれる | 分数の計算方法を解説 分数は小数よりもずっとサボれる |  分数の計算方法を解説 分数は小数よりもずっとサボれる |
分数の計算方法を解説 分数は小数よりもずっとサボれる |  分数の計算方法を解説 分数は小数よりもずっとサボれる |  分数の計算方法を解説 分数は小数よりもずっとサボれる |
分数の計算方法を解説 分数は小数よりもずっとサボれる |  分数の計算方法を解説 分数は小数よりもずっとサボれる | 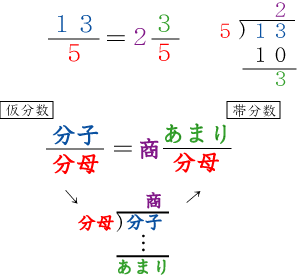 分数の計算方法を解説 分数は小数よりもずっとサボれる |
「帯分数を仮分数に直す方法」の画像ギャラリー、詳細は各画像をクリックしてください。
 分数の計算方法を解説 分数は小数よりもずっとサボれる |  分数の計算方法を解説 分数は小数よりもずっとサボれる |  分数の計算方法を解説 分数は小数よりもずっとサボれる |
 分数の計算方法を解説 分数は小数よりもずっとサボれる |  分数の計算方法を解説 分数は小数よりもずっとサボれる |  分数の計算方法を解説 分数は小数よりもずっとサボれる |
 分数の計算方法を解説 分数は小数よりもずっとサボれる |  分数の計算方法を解説 分数は小数よりもずっとサボれる |  分数の計算方法を解説 分数は小数よりもずっとサボれる |
「帯分数を仮分数に直す方法」の画像ギャラリー、詳細は各画像をクリックしてください。
 分数の計算方法を解説 分数は小数よりもずっとサボれる |  分数の計算方法を解説 分数は小数よりもずっとサボれる |  分数の計算方法を解説 分数は小数よりもずっとサボれる |
 分数の計算方法を解説 分数は小数よりもずっとサボれる | 分数の計算方法を解説 分数は小数よりもずっとサボれる | 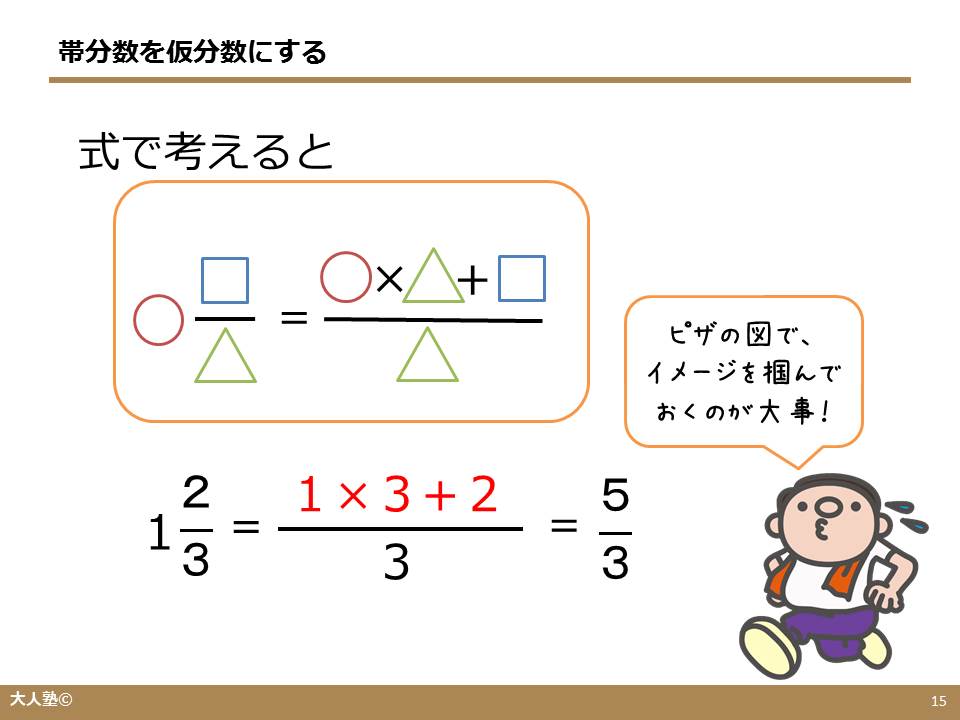 分数の計算方法を解説 分数は小数よりもずっとサボれる |
 分数の計算方法を解説 分数は小数よりもずっとサボれる | 分数の計算方法を解説 分数は小数よりもずっとサボれる | 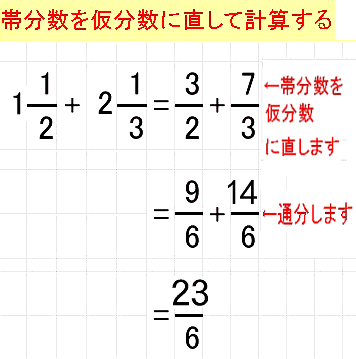 分数の計算方法を解説 分数は小数よりもずっとサボれる |
「帯分数を仮分数に直す方法」の画像ギャラリー、詳細は各画像をクリックしてください。
 分数の計算方法を解説 分数は小数よりもずっとサボれる | 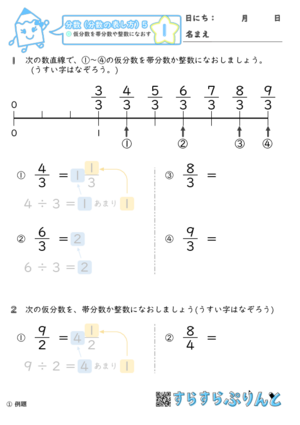 分数の計算方法を解説 分数は小数よりもずっとサボれる |  分数の計算方法を解説 分数は小数よりもずっとサボれる |
 分数の計算方法を解説 分数は小数よりもずっとサボれる | 分数の計算方法を解説 分数は小数よりもずっとサボれる |  分数の計算方法を解説 分数は小数よりもずっとサボれる |
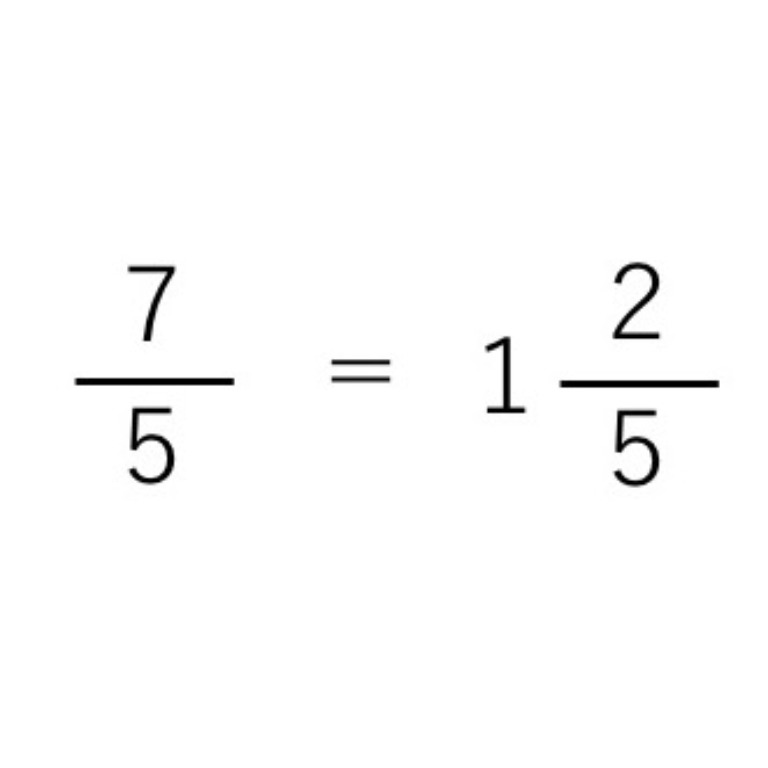 分数の計算方法を解説 分数は小数よりもずっとサボれる |  分数の計算方法を解説 分数は小数よりもずっとサボれる |  分数の計算方法を解説 分数は小数よりもずっとサボれる |
「帯分数を仮分数に直す方法」の画像ギャラリー、詳細は各画像をクリックしてください。
 分数の計算方法を解説 分数は小数よりもずっとサボれる |  分数の計算方法を解説 分数は小数よりもずっとサボれる |  分数の計算方法を解説 分数は小数よりもずっとサボれる |
 分数の計算方法を解説 分数は小数よりもずっとサボれる | 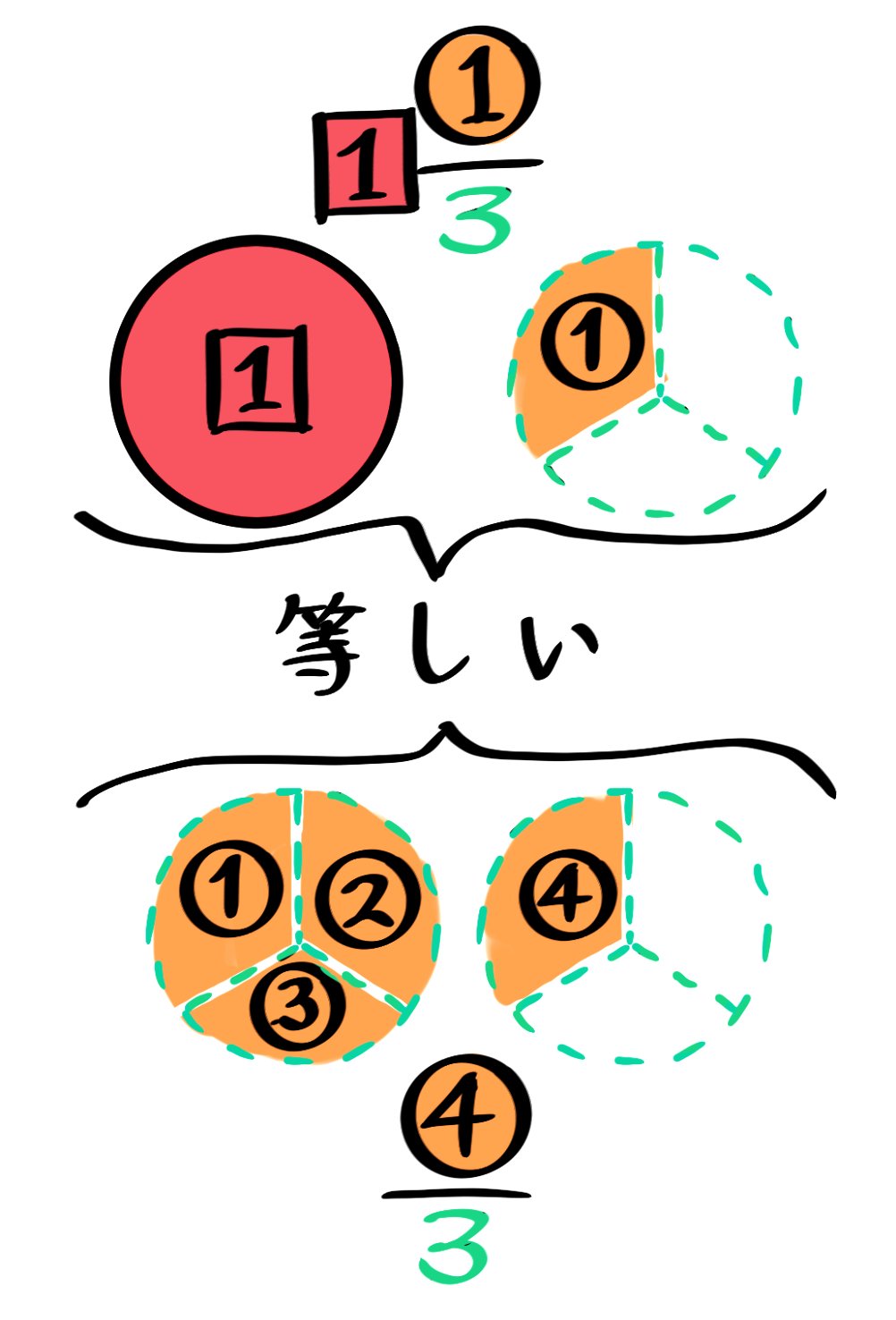 分数の計算方法を解説 分数は小数よりもずっとサボれる |  分数の計算方法を解説 分数は小数よりもずっとサボれる |
 分数の計算方法を解説 分数は小数よりもずっとサボれる |  分数の計算方法を解説 分数は小数よりもずっとサボれる |  分数の計算方法を解説 分数は小数よりもずっとサボれる |
「帯分数を仮分数に直す方法」の画像ギャラリー、詳細は各画像をクリックしてください。
 分数の計算方法を解説 分数は小数よりもずっとサボれる |  分数の計算方法を解説 分数は小数よりもずっとサボれる |  分数の計算方法を解説 分数は小数よりもずっとサボれる |
 分数の計算方法を解説 分数は小数よりもずっとサボれる |  分数の計算方法を解説 分数は小数よりもずっとサボれる | 分数の計算方法を解説 分数は小数よりもずっとサボれる |
 分数の計算方法を解説 分数は小数よりもずっとサボれる | 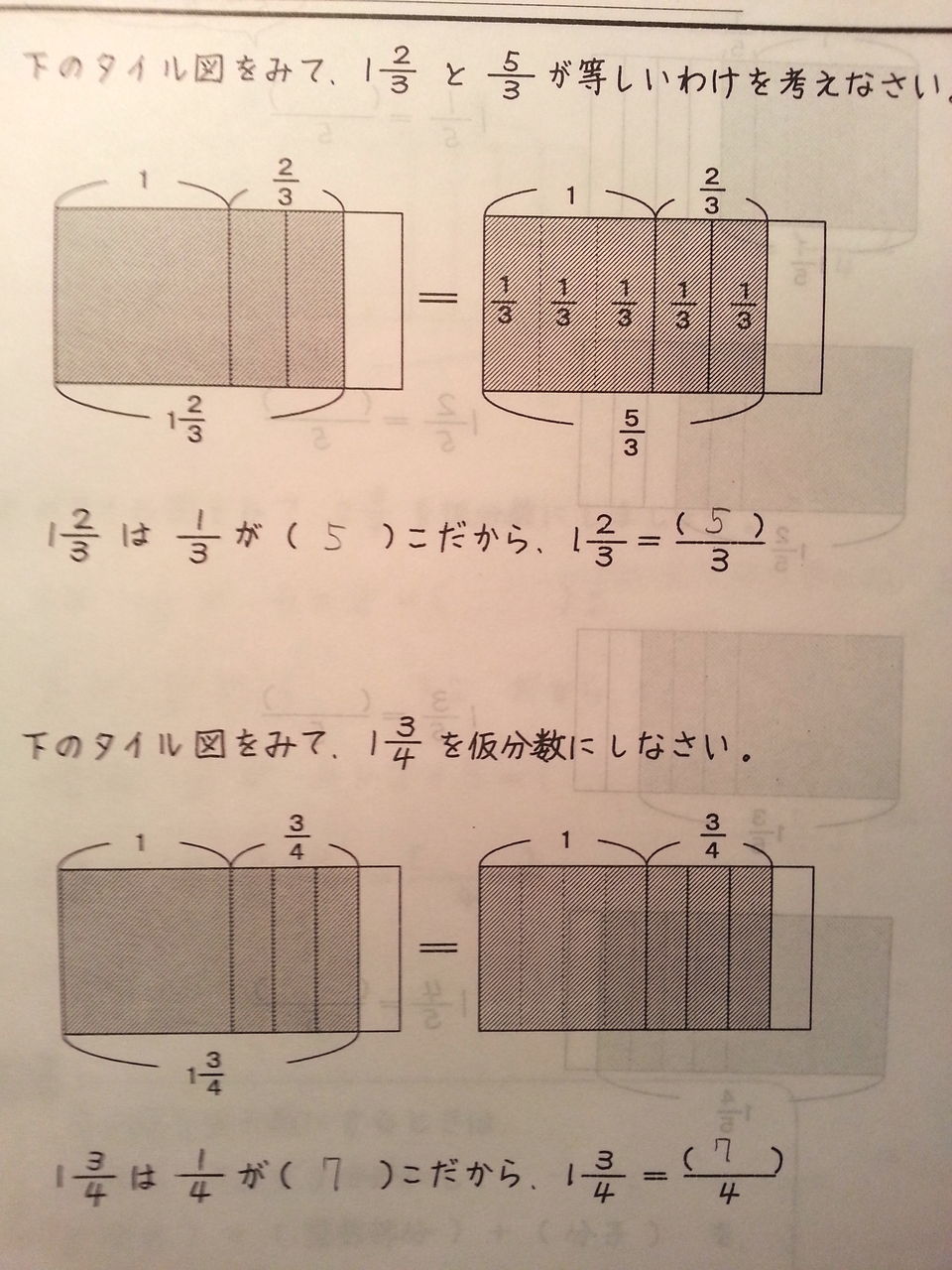 分数の計算方法を解説 分数は小数よりもずっとサボれる | 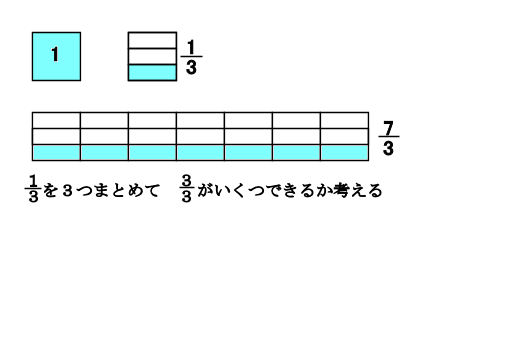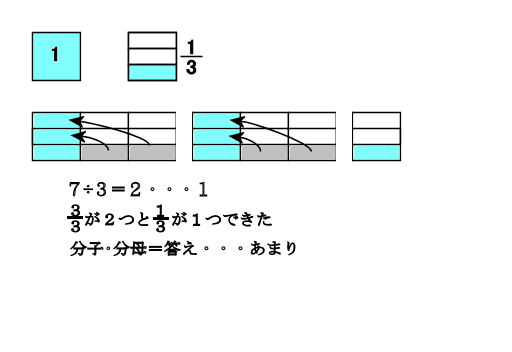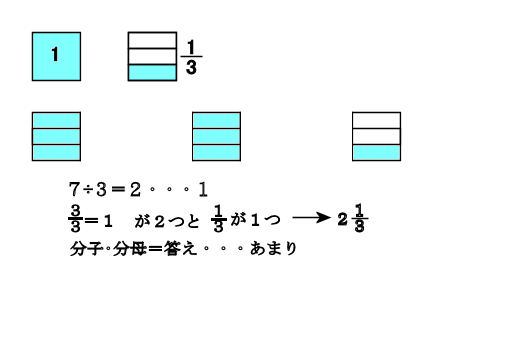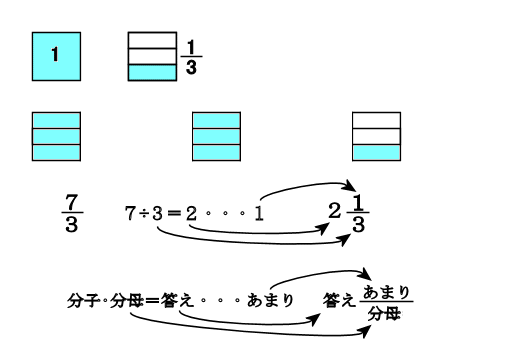 分数の計算方法を解説 分数は小数よりもずっとサボれる |
「帯分数を仮分数に直す方法」の画像ギャラリー、詳細は各画像をクリックしてください。
分数の計算方法を解説 分数は小数よりもずっとサボれる | 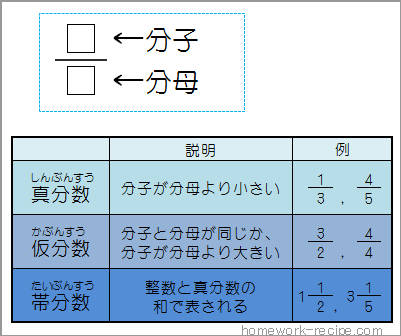 分数の計算方法を解説 分数は小数よりもずっとサボれる |  分数の計算方法を解説 分数は小数よりもずっとサボれる |
 分数の計算方法を解説 分数は小数よりもずっとサボれる | 分数の計算方法を解説 分数は小数よりもずっとサボれる | 分数の計算方法を解説 分数は小数よりもずっとサボれる |
 分数の計算方法を解説 分数は小数よりもずっとサボれる |  分数の計算方法を解説 分数は小数よりもずっとサボれる |  分数の計算方法を解説 分数は小数よりもずっとサボれる |
「帯分数を仮分数に直す方法」の画像ギャラリー、詳細は各画像をクリックしてください。
分数の計算方法を解説 分数は小数よりもずっとサボれる | 分数の計算方法を解説 分数は小数よりもずっとサボれる | 分数の計算方法を解説 分数は小数よりもずっとサボれる |
 分数の計算方法を解説 分数は小数よりもずっとサボれる | 分数の計算方法を解説 分数は小数よりもずっとサボれる |  分数の計算方法を解説 分数は小数よりもずっとサボれる |
分数の計算方法を解説 分数は小数よりもずっとサボれる | 分数の計算方法を解説 分数は小数よりもずっとサボれる | 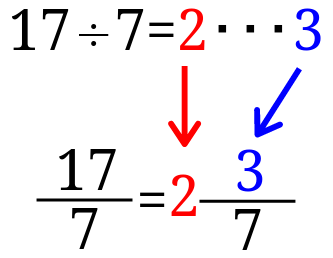 分数の計算方法を解説 分数は小数よりもずっとサボれる |
「帯分数を仮分数に直す方法」の画像ギャラリー、詳細は各画像をクリックしてください。
 分数の計算方法を解説 分数は小数よりもずっとサボれる |  分数の計算方法を解説 分数は小数よりもずっとサボれる | 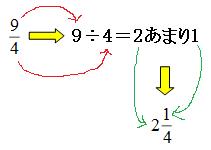 分数の計算方法を解説 分数は小数よりもずっとサボれる |
 分数の計算方法を解説 分数は小数よりもずっとサボれる | 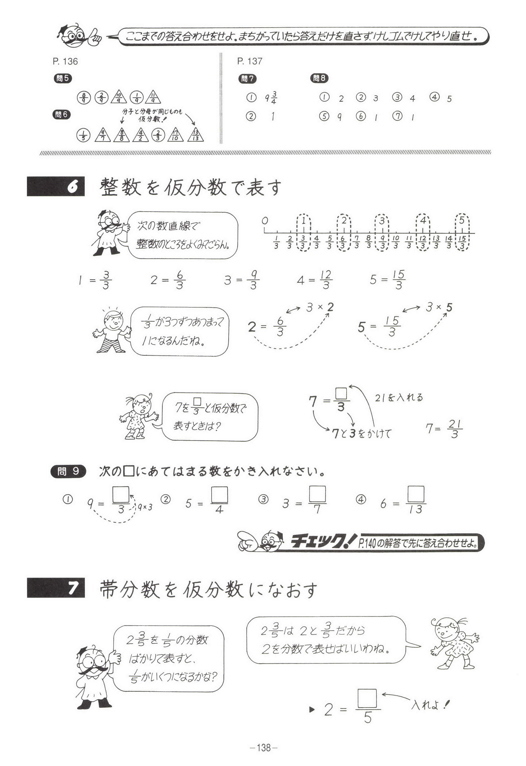 分数の計算方法を解説 分数は小数よりもずっとサボれる | 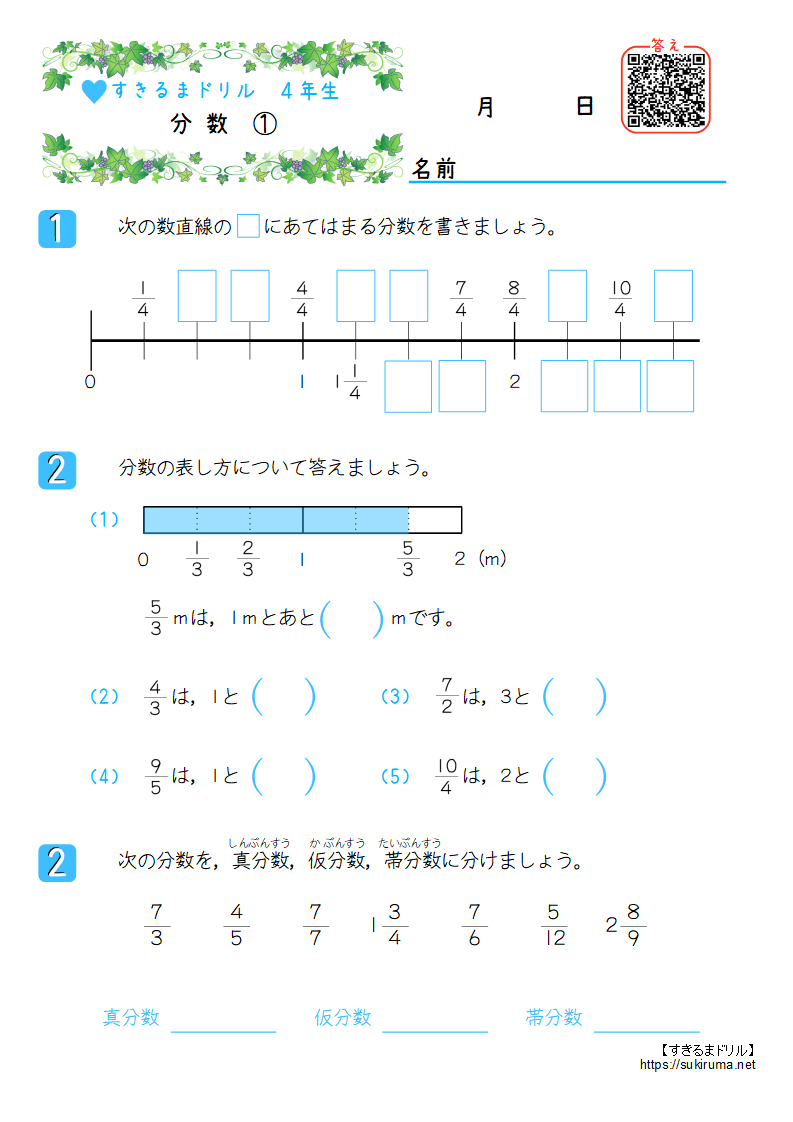 分数の計算方法を解説 分数は小数よりもずっとサボれる |
 分数の計算方法を解説 分数は小数よりもずっとサボれる | 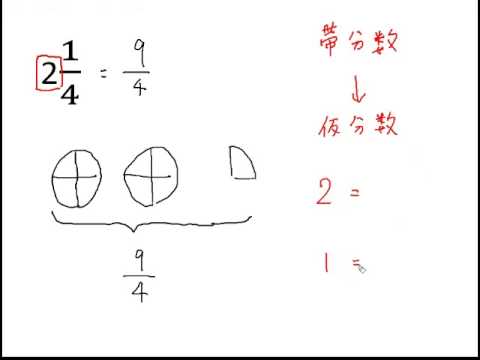 分数の計算方法を解説 分数は小数よりもずっとサボれる |  分数の計算方法を解説 分数は小数よりもずっとサボれる |
「帯分数を仮分数に直す方法」の画像ギャラリー、詳細は各画像をクリックしてください。
 分数の計算方法を解説 分数は小数よりもずっとサボれる |  分数の計算方法を解説 分数は小数よりもずっとサボれる |  分数の計算方法を解説 分数は小数よりもずっとサボれる |
 分数の計算方法を解説 分数は小数よりもずっとサボれる |  分数の計算方法を解説 分数は小数よりもずっとサボれる |
分数の計算 帯分数を仮分数にかえる 算数の公式; 帯分数を仮分数に直す (1 1/2)×(025)×(2 2/3) という問題なんですが、解答を見ていると 途中の式が 2/3×1/4×8/3 = 1 になっていました。 帯分数を仮分数に直すやり方はわかるのですが、 この問題の−の符号がわかりません。
Incoming Term: 帯分数を仮分数に直す方法, 帯分数を仮分数に直す方法 簡単,
コメント
コメントを投稿